La sección áurea es la división de un segmento en dos partes, donde el segmento menor es al segmento mayor, como este es a la totalidad. De esta manera se establece una relación de tamaños con la misma proporcionalidad entre el todo dividido en mayor y menor. Esta proporción o forma de seleccionar proporcionalmente una línea se llama proporción áurea.

Aplicando esta proporción obtenemos la siguiente ecuación que tendremos que resolver

Una de las soluciones de esta ecuación (la solución positiva) es:
Lo sorprendente ahora es calcular el valor que se obtiene al dividir el segmento mayor entre el menor,

Es decir, la relación entre las dos partes en que dividimos el segmento es el número de oro.
Como ya he dicho antes, el número áureo lo encontramos en construcciones y en la naturaleza.
El ejemplo de arquitectura que más impresiona es el de La Gran Pirámide de Keops, donde el cociente entre la altura de uno de los tres triángulos que forman la pirámide y el lado es 2 .

En la naturaleza, aparece la proporción áurea también en el crecimiento de las plantas, las piñas, la distribución de las hojas en un tallo, dimensiones de insectos y pájaros y la formación de caracolas.


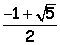



.JPG)









